
If the data support only the inclusion of a random slope for age.orth.1, then you don't have much choice. However, depending on your data, your model may or may not support the inclusion of two random slopes - one for age.orth.1 and the other for age.orth.2.
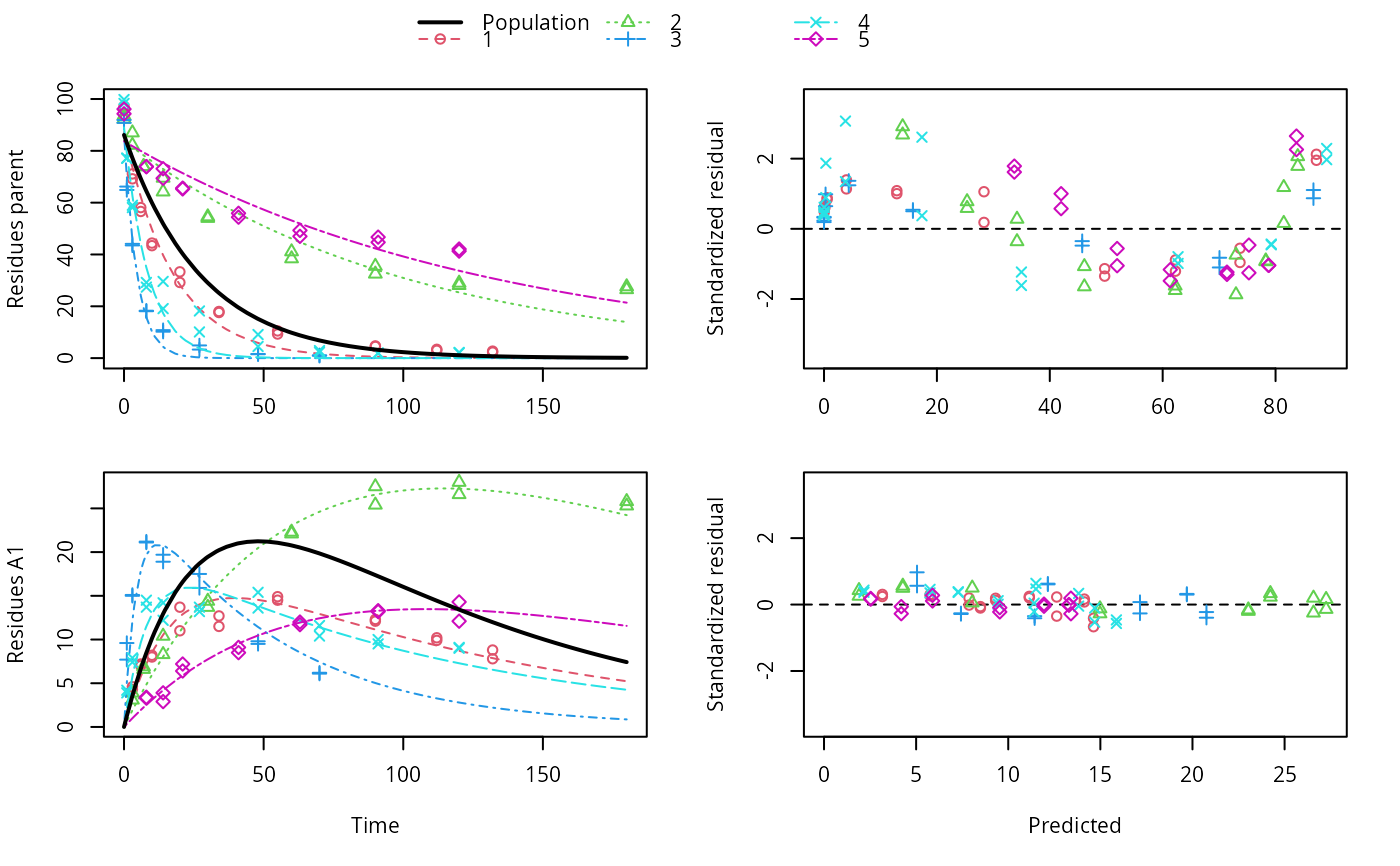
In principle, both the slope for age.orth.1 and age.orth.2 can vary across the persons represented by the ones included in your study. Then: model <- lmer(affect ~ age.orth.1*group + age.orth.2*group + My_data $age.orth.2 <- poly(my_data$day, 2, raw=FALSE) # orthogonal version of day^2 If you need to include random slopes just for the linear but not for the quadratic effect of age in your latter model, best to add your orthogonal polynomials to your dataset and give them appropriate names: my_data $age.orth.1 <- poly(my_data$day, 2, raw=FALSE) # orthogonal version of day You can fit models like this for raw polynomials: model <- lmer(affect ~ poly(day,2, raw=TRUE)*group +Īnd like this for orthogonal polynomials: model <- lmer(affect ~ poly(day,2, raw=FALSE)*group + Orthogonal <- poly(day, 2, raw=FALSE) # orthogonal versions of day and day^2Ĭor(raw) # high correlation between day and day^2Ĭor(orthogonal) # no correlation between orthogonal versions of day and day^2 Raw <- poly(day, 2, raw=TRUE) # raw contains day and day^2 for one person
#Rcode nlme code#
This code - for one person - will give you more insights: day <- 1:28 # day predictor for one person Orthogonal polynomials are preferred to raw polynomials as they combine to produce the same fit to the data (e.g., quadratic) for each person, while averting collinearity problems. The problem with introducing multiple raw polynomials in your model is that they can be highly correlated with each other, thereby creating collinearity problems for the model. Typically, you'll see NOERROR (RCODE:0) when doing most of your successful browsing, all of the other return codes are consider errors. Each return code has its own purpose in the DNS infrastructure. In your model, these raw polynomials are represented by the terms day and I(day^2). The following table explains the DNS return codes that can be returned when doing a DNS query and may appear in your logs. For example, day (which is day raised to power 1) and day squared (which is day raised to power 2) are raw polynomials.

Raw polynomials of your day variable are simply powers of that variable. if I have to rescale, how does one go about? It has to do with the quadratic term, I know that, but any suggestions as to how I should then rescale are more than welcome. is it a serious issue in the first place, or can I more or less ignore it,Ĥ.
Here comes the R code used in this tutorial: library (nlme). If it is correct, if I run it, it says that the model is nearly unidentifiable: very large eigenvalue. A video showing basic usage of the 'lme' command (nlme library) in R. Note: I added the double || in an attempt to get the covariance structure 'unstructured', as an enlightened mind in our department said I should. is the following the correct way model <- lmer(affect ~ group + day + I(day^2) + group * day + group * I(day^2) + should I separately code random slopes for time^2, or is that nonsense, and if so, 2. My question is both theoretical and practical: 1. I want to build a linear mixed model (on daily diary data: 5x a day, 28 days, so 140 measurements for 110 persons in two treatment groups) as follows:Īffect(dep.var) = Group + Time + Time^2 + group * time + group * time^2 + random.interceptsubjects + random.slopetime Region_id + fiscal_year + (1|city_name), mydata)įor parameter effect size (standardized beta weights):įor effect size for whole model (variation in linear mixed effects models):ġ-var(residuals(model1))/(var(model.response(model.I've worked through quite some documentation about both the nlme and lme4 package, (and quite some fora) but am still unsure whether I'm doing the right thing. Nn_cent + distance + city_net_exp + county_pop_avg_per_hh + county_vcncy + The lme4 model is: model1<-lmer(logh_production ~ growth + p_will + subsidy + trt_grp + compliance +

I have connected to the domain from several XP computers. A good choice is the ‘nlme ()’ function in the ‘nlme’ package (Pinheiro and Bates, 2000), although the syntax may be cumbersome, at times. I have added the dns server address to the nic properties. In order to account for the clustering of observations, we switch to a Nonlinear Mixed-Effect model (NLME).
#Rcode nlme windows#
I cannot connect to Windows 2008 standard domain controller. While working with a tutor, he ran the same model in lme4 and obtained standardized coefficients and model effect size using the following codes. I can connect via the run window and view files. I have fit a longitudinal random effects model using nlme and I prefer nlme because I can get p-values.


 0 kommentar(er)
0 kommentar(er)
